Una curiosa e interesante propiedad de los números naturales. El cuadrado de la suma de los n primeros números naturales es igual a la suma de los cubos de dichos números.
( 1 + 2 + 3 + … + n )2 = 13 + 23 + 33 + … + n3
Comprobación para n=1, 2, 3, 4 y 5:
| 12=1 |
13=1 |
| (1+2)2=32=9 |
13+23=1+8=9 |
| (1+2+3)2=62=36 |
13+23+33=1+8+27=36 |
| (1+2+3+4)2=102=100 |
13+23+33+43=1+8+27+64=100 |
| (1+2+3+4+5)2=152=225 |
13+23+33+43+53=1+8+27+64+125=225 |
| . . . |
. . . |
Demostración gráfica para n=4.
 |
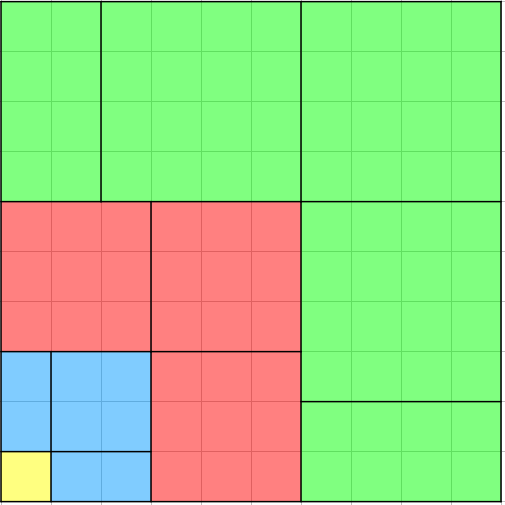La longitud del lado del cuadrado completo es: 1+2+3+4=10. El área del cuadrado completo es: (1+2+3+4)2=102=100. |
| Hay un cuadrado de lado 1. Su área es 1. |
| Juntando las dos mitades, hay dos cuadrados de lado 2. El área de los dos es 2·22=23. |
| Hay tres cuadrados de lado 3. El área de los tres es 3·32=33. |
| Juntando las dos mitades, hay cuatro cuadrados de lado 4. El área de los cuatro es 4·42=43. |
| El área del cuadrado completo, sumando las área de todos los cuadrados es: 1·12+2·22+3·32+4·42=13+23+33+43=1+8+27+64=100. |
