Un cuadrado mágico multiplicativo de orden n es un conjunto de números dispuestos en n filas y n columnas, de forma que el producto de todas las filas, de todas las columnas y de las dos diagonales es siempre la misma. A este producto se le llama constante mágica.
La constante mágica se puede calcular multiplicando todos los números utilizados y calculando la raíz de índice n del producto obtenido.
A partir del cuadrado mágico de orden 3, se pueden construir un cuadrado mágico multiplicativo con potencias de la misma base y exponente los números que aparecen en el cuadrado.
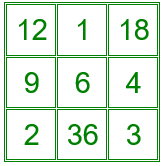
Se puede construir un cuadrado mágico multiplicativo de orden 3 con los divisores de 36.
Div(36) = { 1 , 2 , 3 , 4 , 6 , 9 , 12 , 18 , 36 }
Constante mágica:
El producto de las tres filas, las tres columnas y las dos diagonales principales es 216
Y el cuadrado mágico multiplicativo de orden 3 con los divisores de 36 es:
