El número de oro
Su descubrimiento se remonta al siglo V a. C., en la época de la Grecia Clásica, en la que era muy utilizado en arquitectura y escultura. Sin embargo hubo que esperar hasta el siglo XIX para conocerlo por la sexta letra del abecedario griego “Φ”, inicial del nombre del escultor griego Fidias (490-431 a.C.) que lo utilizó en sus obras.
Euclides (325-265 a.C.), en el siglo III a.C. lo utiliza en sus Elementos. En el año 1500 Luca Pacioli (1447-1517) lo reconocía como La divina Proporción. El nombre de Número de Oro o Proporción Áurea se le da en es siglo XIX en Alemania.
Posiblemente su descubrimiento se debe al estudio de las proporciones y de la medida de un segmento. Vamos a dividir un segmento de longitud una unidad en dos partes, de forma que la razón entre la parte mayor y la parte menor sea igual a la razón entre el total y la parte mayor. A esta forma de dividir un segmento se le conoce como proporción o sección áurea.
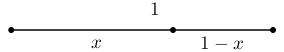
De la proporción deseada resulta la ecuación de segundo grado:
![]()
De las dos soluciones de la ecuación, solo será válida la solución positiva. Las medidas de las dos partes en que queda dividido el segmento, «x» y «1-x», son:
![]()
El número de oro, Φ, es la razón entre la parte mayor y la menor:
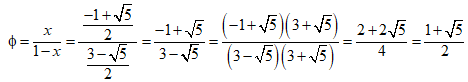
El número de oro es un número irracional, es decir, está formado por infinitas cifras decimales no periódicas. Hoy en día, es fácil calcular el número de oro con una gran cantidad de cifras decimales utilizando un ordenador.
Φ=1.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748 …





















