El número e
El número e fue descubierto por John Napier, (1550-1617), en el siglo XVI, es la base de los logaritmos neperianos (o logaritmos naturales). Sin embargo fue Leonhard Euler, (1707-1783), quién le puso su inicial como nombre en 1728.
Euler demostró que el número e es irracional. El francés Charles Hermite, (1822-1901), demostró en 1973 que es un número trascendente, es decir, que no se puede construir con regla y compás y que no se puede obtener como solución de ninguna ecuación con coeficientes racionales.
Se puede definir el número e como el límite cuando n tiende a infinito de la sucesión:
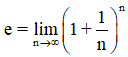
Si calculamos varios términos de la sucesión, obtenemos:
| n = 1 | 2 | n = 102 | 2.7048138294215 | |||
| n = 2 | 2.25 | n = 103 | 2.7169239322359 | |||
| n = 3 | 2.370370370370 | n = 104 | 2.7181459268252 | |||
| n = 4 | 2.4414062500 | n = 105 | 2.7182682371745 | |||
| n = 5 | 2.48832 | n = 106 | 2.7182804693194 | |||
| n = 6 | 2.5216263717421 | n = 107 | 2.718281692545 | |||
| n = 7 | 2.5464996970407 | n = 108 | 2.7182818148676 | |||
| n = 8 | 2.5657845139503 | n = 109 | 2.7182818270999 | |||
| n = 9 | 2.5811747917132 | n = 1010 | 2.7182818283231 | |||
| n = 10 | 2.5937424601 | . . . | . . . |
Hoy en día es fácil calcular el número e con una gran cantidad de cifras decimales utilizando un ordenador.
e=2.7182818284590452353602874713526624977572470936999595749669676277240766303535475945713821785251664274…





















