El pentágono regular y el número de oro
En un pentágono de 1 cm de lado se encuentran los dos triángulos isósceles anteriores que verifican que el cociente de sus lados es el número de oro. En cualquier otro pentágono regular se encuentran triángulos semejantes.
En cualquier pentágono regular, el cociente entre la longitud de una diagonal y la longitud del lado es el número de oro. Si el lado del pentágono mide 1 cm, la longitud de la diagonal es el número de oro.

Al trazar las diagonales en un pentágono cualquiera, todos los triángulos que se forman son triángulos semejantes a alguno de los dos anteriores.
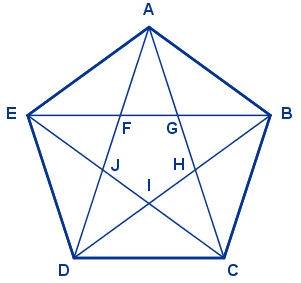
En esta figura solo hay cuatro longitudes distintas de segmentos, AC, AB, AG y FG, que verifican:
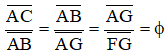
Y solamente tres ángulos distintos: 36º, 72º y 108º.





















