Un grafo es conexo si cada par de vértices están unidos por un camino.

Un grafo conexo es euleriano si y solo si cada vértice tiene grado par.

Si un grafo contiene un camino euleriano, entonces todos los vértices tienen grado par o solamente dos vértices tienen grado par. En este caso, para construir el camino euleriano hay que empezar por uno de los vértices de grado impar y acabar en el otro.

En el siguiente grafo, el vértice A tiene grado 1 y el vértice B tiene grado 3. No puede ser un grafo euleriano, pero sí se puede construir un camino euleriano empezando por el vértice A y acabando por el vértice B o al contrario.

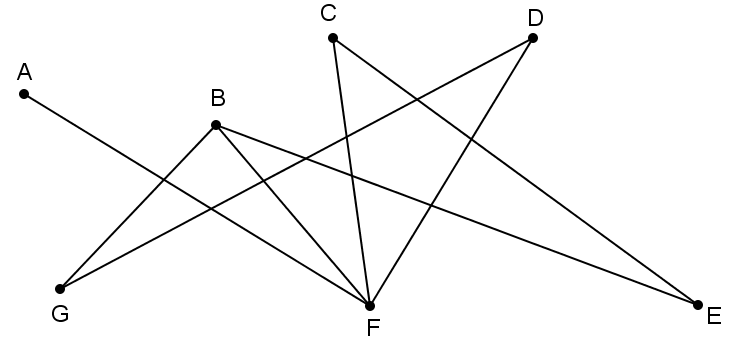
En el siguiente grafo todos los vértices tienen grado par, es un grafo euleriano. Se puede construir un circuito euleriano, empezando y acabando en un mismo vértice.

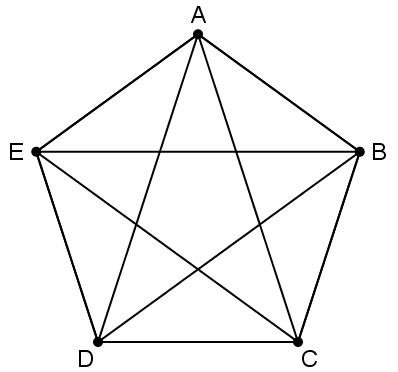
En el problema de los puentes de Königsberg, realizar el recorrido propuesto, equivale a construir la siguiente figura sin levantar el lápiz del papel y sin pasar dos veces por la misma línea, es decir, construir un circuito euleriano. Pero no se puede construir este camino porque los cuatro vértices del grafo tienen grado impar, por tanto, no es posible recorrer la ciudad a pie, pasando una sola vez por cada uno de los puentes y volviendo al punto inicial.

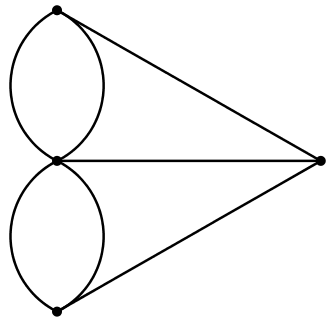
Utiliza estos resultados para resolver la siguiente actividad propuesta en este blog con anterioridad:

Sin levantar el lápiz del papel