La sucesión de Fibonacci y el número de oro
Si en la sucesión de Fibonacci se divide cada uno de los términos por el anterior, se obtiene una nueva sucesión cuyo límite es el número de oro; Φ=1.6180339887.
Ya se observa una aproximación en los primeros cocientes:

Pero este resultado se puede demostrar de la siguiente forma:
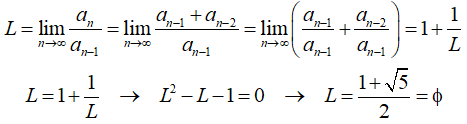
La ecuación tiene dos soluciones, una positiva y otra negativa. Como todos los cocientes de la sucesión son positivos, el valor del límite es la solución positiva.





















