Se conoce como ladrillo de Euler a un ortoedro en el que las longitudes de las aristas y de las diagonales de las caras son números naturales. Si además, el máximo común divisor de las aristas es 1, el ortoedro se llama ladrillo de Euler primitivo.

El ladrillo de Euler más pequeño lo descubrió, en el año 1719, el matemático e informático alemán Paul Halcke (1662-1731). Es el siguiente:

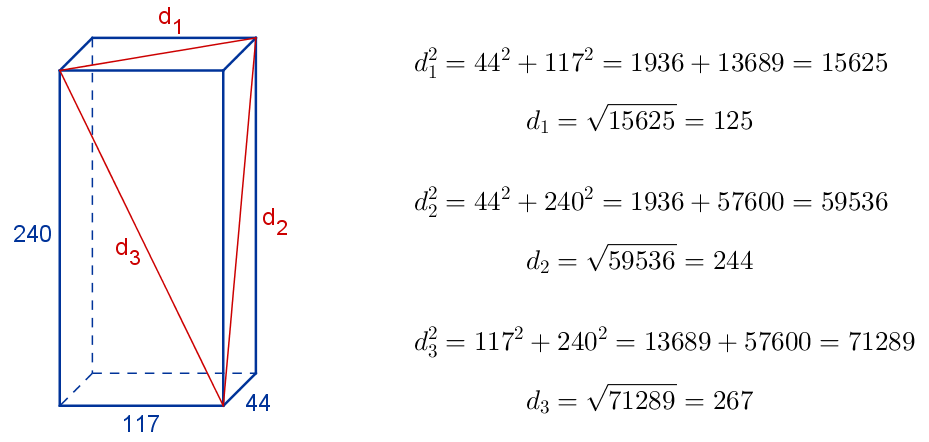
Otros ladrillos de Euler tienen por longitudes de aristas y diagonales:

Aristas: 85, 135, 720.   Diagonales: 157, 725, 732.

Aristas: 140, 480, 693.   Diagonales: 500, 707, 843.

Aristas: 160, 231, 792.   Diagonales: 281, 808, 825.

Aristas: 240, 252, 275.   Diagonales: 348, 365, 373.

En estos ortoedros, la diagonal mayor no es un número natural. No se ha encontrado todavía el ortoedro con las longitudes de las aristas, las diagonales de las caras y la diagonal mayor, números naturales. A este ortoedro se le llamaría ortoedro perfecto o ladrillo perfecto de Euler.