Distancia
En un triángulo rectángulo se construye un cuadrado de lado la longitud de la hipotenusa. Calcula la distancia del vértice del ángulo recto del triángulo al centro del cuadrado.
Adicción Matemática Blog
El espía
Un espía principiante quiere entrar en el campamento del enemigo. Se camufla entre la vegetación cercana a la entrada para escuchar la contraseña que le dicen los que entran, al vigilante de la puerta.
Llega la primera persona y el vigilante le dice «ocho». El visitante le responde «cuatro» y le permite pasar.
Llega una segunda persona y el vigilante le dice «catorce». El visitante responde «siete» y también pasa al campamento.
Llega una persona más y el vigilante le dice «dieciocho». El visitante responde «nueve» y también pasa al campamento.
Entonces el espía, convencido de haber descubierto la contraseña, sale de su escondite y se acerca a la puerta del campamento enemigo. El vigilante le dice «veinte» y el espía responde, con mucha seguridad, «diez». El vigilante comenta «no es correcto, la respuesta es seis»; llama a los guardias y el espía es capturado.
¿Cuál es el secreto de la contraseña?
Espiral triangular áurea
Esta espiral triangular tiene también un crecimiento áureo. Se construye con los dos triángulos isósceles de proporciones áureas. El cociente entre el radio de cada arco y el radio del arco anterior es el número de oro.
Haz «click» sobre la imagen para abrir la construcción de GeoGebra.
Atriftaloide
Este tipo de curvas fue estudiado por el geólogo irlandés Samuel Haughton (1821-1897) y por el físico y matemático irlandés John Sealy Edward Townsend (1868-1957).
Haz «click» sobre la imagen para abrir la construcción de GeoGebra.
El número 36
En una entrada anterior aparece un resultado y su demostración de que todos los números naturales son interesantes en Matemáticas. Otro de los números interesantes es el número 36 porque aparece en las siguientes sucesiones y situaciones:
| • Es el octavo número triangular: | • Es el sexto número cuadrado perfecto: |
| 1 , 3 , 6 , 10 , 15 , 21, 28 , 36 , … | 1 , 4 , 9 , 16 , 25 , 36 , … |
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36 |
1 + 3 + 5 + 7 + 9 + 11 = 36 |
• Aparece como medida de ángulos en los triángulos isósceles con proporciones áureas.
 |
 |
| Los ángulos miden: 36º, 2·36º, 2·36º. | Los ángulos miden: 3·36º, 36º, 36º. |
Triángulo de Reutersvärd
Oscar Reutersvärd, (1915-2002), es conocido como «el padre de las figuras imposibles».
El pentágono regular y el número de oro
En un pentágono de 1 cm de lado se encuentran los dos triángulos isósceles anteriores que verifican que el cociente de sus lados es el número de oro. En cualquier otro pentágono regular se encuentran triángulos semejantes.
En cualquier pentágono regular, el cociente entre la longitud de una diagonal y la longitud del lado es el número de oro. Si el lado del pentágono mide 1 cm, la longitud de la diagonal es el número de oro.
Al trazar las diagonales en un pentágono cualquiera, todos los triángulos que se forman son triángulos semejantes a alguno de los dos anteriores.
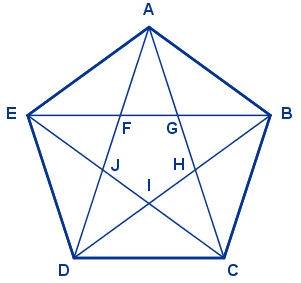
En esta figura solo hay cuatro longitudes distintas de segmentos, AC, AB, AG y FG, que verifican:
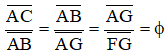
Y solamente tres ángulos distintos: 36º, 72º y 108º.
Cuadrado mágico de orden 8
La constante mágica de un cuadrado de orden 8 se puede calcular sumando todos los números utilizados y dividiendo la suma por 8. Por ejemplo, la constante mágica de un cuadrado de orden 8 con los sesenta y cuatro primeros números naturales es:
La suma de las ocho filas, las ocho columnas y las dos diagonales principales es 260.
Para construir un cuadrado mágico de orden 8 con los sesenta y cuatro primeros números naturales, se colocan los números ordenados como aparecen en el cuadrado de la izquierda. A continuación se intercambian los números de los grupos coloreados, invirtiendo el orden de filas y columnas como aparece en la figura.
Polígonos estrellados y estrellas en un decágono regular
Un polígono regular estrellado se obtiene uniendo los vértices de un polígono regular de forma no consecutiva, empezando y acabando por el mismo y pasando solamente una vez por los demás.
En en un decágono regular se pueden construir un polígono regular estrellado y tres estrellas.
• Uniendo dos vértices dejando un vértice intermedio entre ellos no se puede construir un polígono regular estrellado, se obtienen dos pentágonos. Pero sí se puede construir una estrella con los dos pentágonos.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
• Uniendo dos vértices dejando dos vértices intermedios entre ellos sí se obtiene un polígono regular estrellado.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
• Uniendo dos vértices dejando tres vértices intermedios entre ellos no se puede construir un polígono regular estrellado, se obtienen dos polígonos regulares estrellados de cinco vértices. Pero sí se puede construir una estrella con estos dos polígonos.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
María Gaetana Agnesi
En la dedicatoria de su libro a la emperatriz María Teresa de Austria: «Si en algún momento puede excusarse la temeridad de una mujer, que se atreve a aspirar a las sublimidades de una ciencia que no conoce límites, ni siquiera los de la infinitud misma, ciertamente debería ser en este período, en el que reina una mujer. En esta época toda mujer debería esforzarse, y empeñarse en promover la gloria de su sexo«.
María Gaetana Agnesi.
Milán, 16 de mayo de 1718 – Milán, 9 de enero de 1799.
Matemática italiana.
Escribió el libro “ Instituzioni Analitiche” en el que trata conjuntamente cálculo diferencial e integral. Una curva algebraica lleva su nombre, la curva de Agnesi.
