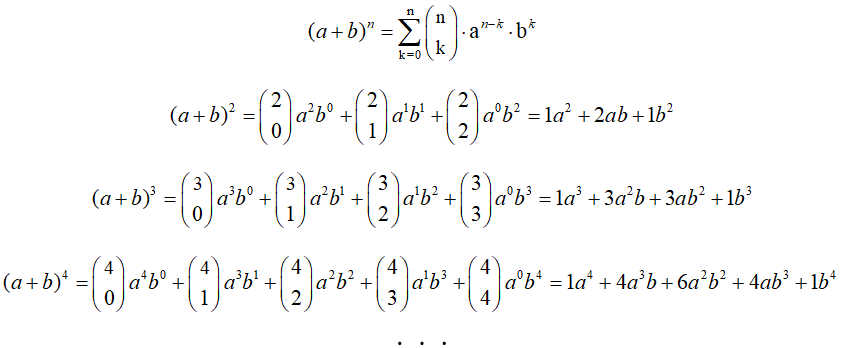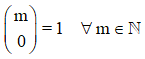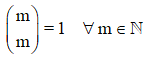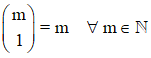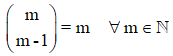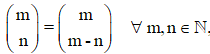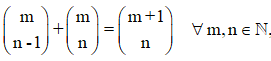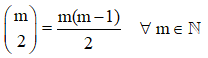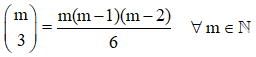Triángulo de Pascal
Se llama factorial de un número natural n al producto de los n primeros números naturales. Se representa por n!.
![]()
Para el número 0 no tiene sentido esta definición. Se define factorial de 0 como 1. 0!=1.
Se llama número combinatorio, m sobre n, con m≥n, a la expresión:
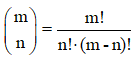
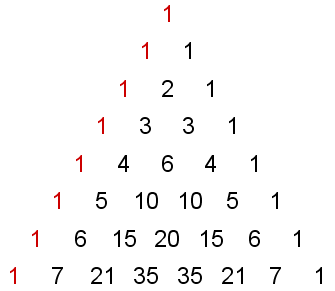
Si se colocan los números combinatorios formando el siguiente triángulo, conocido como triángulo de Pascal o triángulo de Tartaglia, se obtiene un método rápido para calcularlos. En este triángulo, cada número combinatorio se obtiene sumando los dos que tiene sobre él.
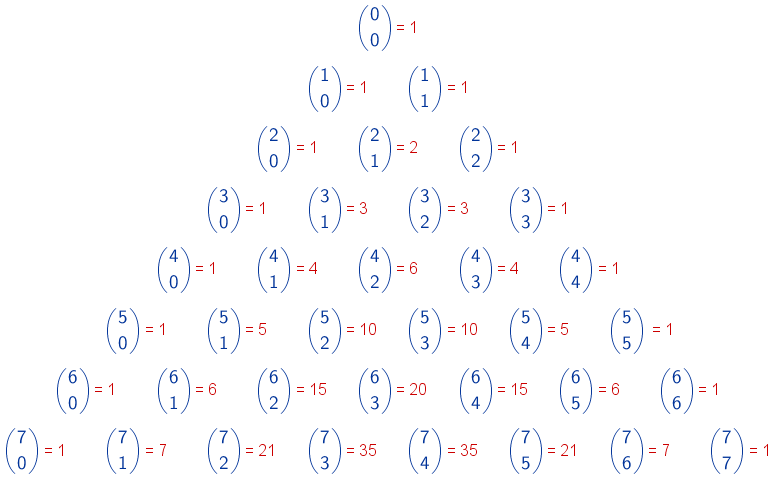
En el Triángulo se pueden comprobar las propiedades de los números combinatorios:
| 1. El primer elemento de cada fila es igual a 1.
|
2. El último elemento de cada fila es igual a 1.
|
|
3. El segundo elemento de cada fila es igual al número superior del número combinatorio.
|
4. El penúltimo elemento de cada fila es igual al número superior del número combinatorio.
|
|
|
5. Cada fila del triángulo se lee igual de izquierda a derecha que de derecha a izquierda.
|
6. Cada número combinatorio se obtiene sumando los dos que tiene sobre él.
|
|
|
7. El tercer elemento de cada fila es un número triangular.
|
8. El cuarto elemento de cada fila es un número tetraédrico.
|
9. La suma de todos los números combinatorios que tienen como número superior m, es igual a 2m.
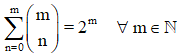
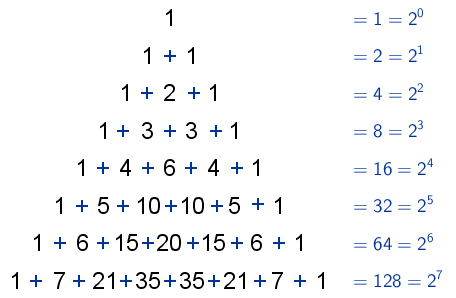
10. Si en cada una de las filas del triángulo de Tartaglia, se alternan consecutivamente signos de sumar y restar, y se realizan las operaciones resultantes, el resultado es 0.
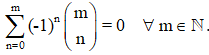
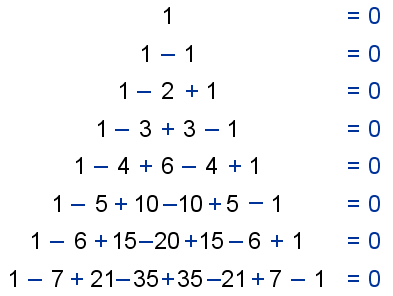
11. Sucesión de Fibonacci. Al sumar los números contenidos en cada una de las rectas se obtiene la sucesión de Fibonacci.
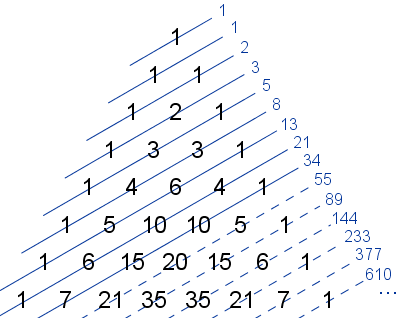
12. Binomio de Newton. Cada una de las filas del Triángulo de Pascal contiene todos los coeficientes del binomio de Newton (a+b)n.