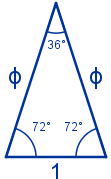
Triángulo isósceles con proporciones áureas I
No existe un triángulo escaleno con las proporciones áureas, pero si existe un triángulo isósceles en el que la razón entre los lados iguales y el lado distinto sea el número de oro, es decir, un triángulo semejante al triángulo cuyos lados miden f, f y 1.
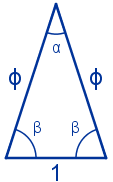
Vamos a calcular los ángulos. Se calcula el ángulo α con el teorema del coseno.
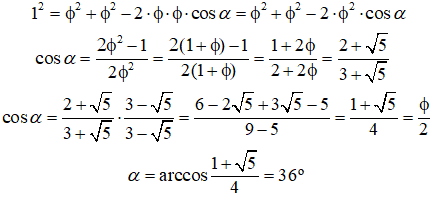
Y ahora se pueden calcular los dos ángulos iguales.
![]()
El triángulo buscado es cualquier triángulo semejante al triángulo siguiente: