Construcción de un eneágono regular inscrito en una circunferencia
Construcción, con regla y compás, de un eneágono regular inscrito en una circunferencia.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
enero 2021
Ratones y gatos
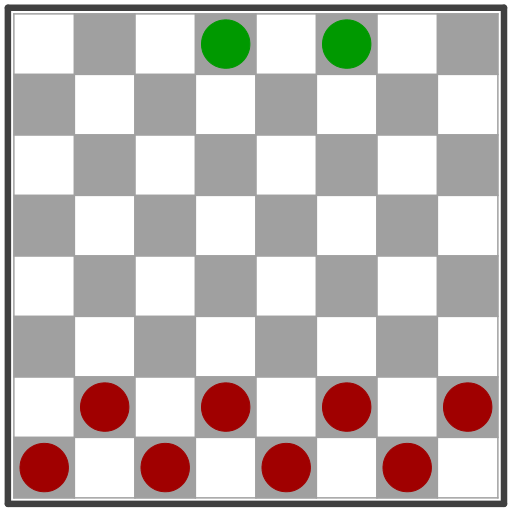
Juego para dos jugadores. Los ocho gatos (fichas rojas) tienen que acorralar a los dos ratones (fichas verdes).
Un jugador mueve los gatos y otro los ratones. Tanto unos como otros solo se pueden mover una casilla en diagonal, no están permitidos los desplazamientos horizontales ni verticales. Los gatos siempre se mueven hacia adelante, los ratones pueden moverse hacia adelante y hacia atrás.
Los gatos tienen que acorralar a los ratones y que éstos no puedan moverse. Los ratones tienen que intentar escapar de los gatos.
(Haciendo «click» sobre la imagen puedes practicar con el juego realizado en GeoGebra).
E. T. Bell
«Los errores y dificultades no resueltos en el pasado de las Matemáticas siempre han sido las oportunidades de su futuro».
Eric Templo Bell.
Peterhead, 7 de febrero de 1885. Watsonville – 21 de diciembre de 1960.
Matemático y escritor de ciencia ficción escocés.
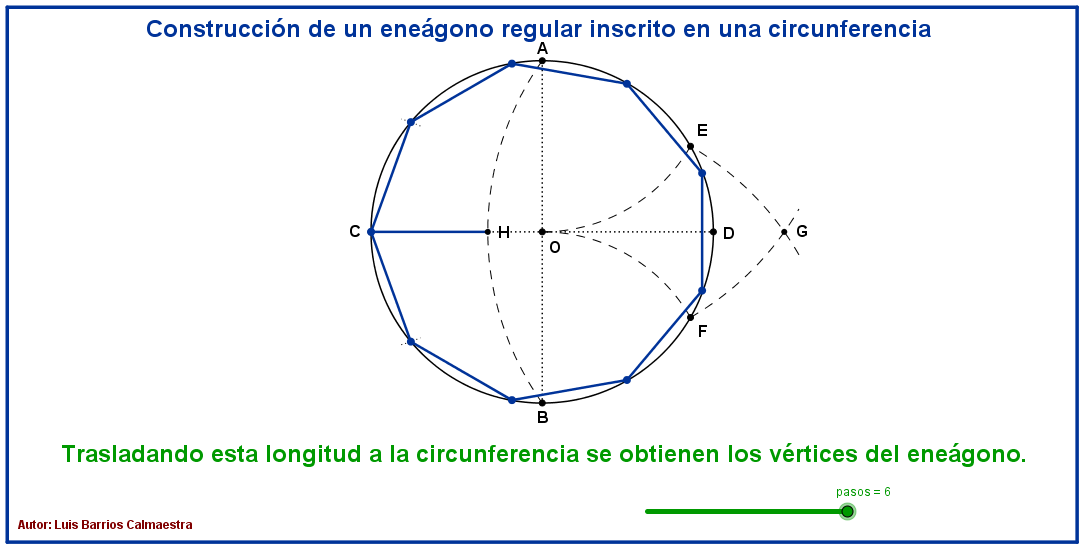
Aproximaciones por defecto y por exceso de π. Método de Arquímedes.
El matemático griego Arquímedes, (287 a.C.-212 a.C.), fue el primero en idear un procedimiento matemático para calcular el valor de π, obteniendo que estaba comprendido entre 3+10/71=223/71 y 3+1/7=22/7.
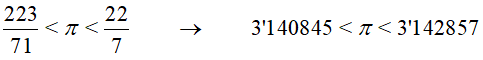
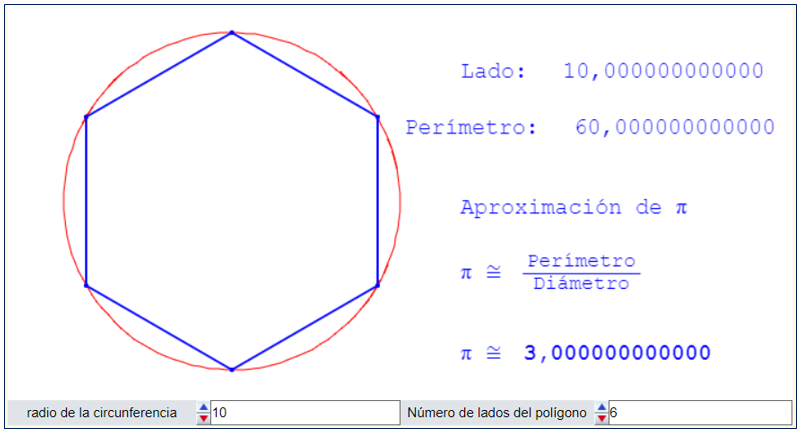
El método usado por Arquímedes consistía en circunscribir e inscribir polígonos regulares de n lados en circunferencias y calcular el perímetro de dichos polígonos. Empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.
(Haciendo «click» con el ratón sobre cualquiera de las imágenes se puede abrir una miscelánea de la Red Educativa Digital Descartes, en la que se puede comprobar de forma interactiva, modificando los parámetros de las pestañas de la barra inferior, como varía el cociente entre el perímetro del polígono regular y el diámetro de la circunferencia, en los polígonos inscritos y circunscritos, por separado o de forma conjunta).
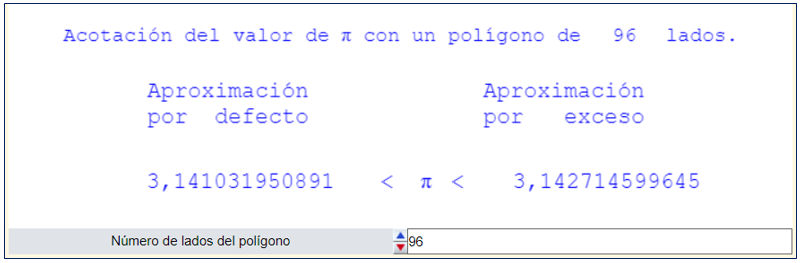
Con los instrumentos de cálculo actuales la acotación sería:
Primeras aproximaciones del número π.
• En el Papiro de Rhind, (papiro egipcio, de 6 m. de longitud y 32 cm. de ancho, escrito por el escriba Ahmes a mediados del siglo XVI a.C., copiado de un documento del siglo XIX a.C.), se dan instrucciones para calcular el área de un círculo “Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. Este cuadrado tiene igual área que el circulo”. Se puede deducir que el valor de π es 256/81, aproximadamente 3’16.
• En Babilonia, aproximadamente en 1600 a. C., medían la circunferencia de un círculo como tres veces el diámetro y el área como un doceavo del cuadrado de la circunferencia, lo cual es correcto para una estimación de π a 3.
• En la Tablilla de Susa, (tablilla con problemas de Geometría del segundo milenio antes de Cristo, aproximadamente del año 1600 a. C.), en Mesopotamia, los babilonios utilizaban como valor de π, 3+1/8=3’125.
• En la Biblia, (libro primero de los Reyes, capítulo 7, versículo 23 y en el libro segundo de las Crónicas, capítulo 4, versículo 2), se puede leer la descripción de un depósito de agua para el palacio del Rey Salomón: «Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo. Tenía cinco codos de altura y a su alrededor un cordón de treinta codos«. De aquí se deduce que se da a π el valor 3.
Manzanas y peras
Entre manzanas y peras he comprado 12 piezas de fruta por 99 céntimos. Si una manzana cuesta tres céntimos mas que una pera y he comprado más manzanas que peras, ¿cuántas piezas de fruta de cada tipo he comprado y cúal es el precio de cada una?
El secreto de las rectas paralelas
Es un problema social.
Diferencias muy curiosas
Comprueba con tu calculadora:
Universo matemático. Capítulo 4.
Fermat: el margen más famoso de la historia.
La serie “Universo matemático” fue creada por el profesor Antonio Pérez Sanz y producida por RTVE en 2000. Ahora RTVE la pone a disposición de los docentes a través de su menú “a la carta”.
Haz click sobre la imagen inferior para verlo.
Triángulo equilátero inscrito en cuadrado
En un cuadrado de 1cm2 de superficie, se inscribe un triángulo equilátero según aparece en la figura. Calcula el lado del triángulo.
