Tres esferas
M.C. Escher. Tres esferas. 1945.
Xilografía. 16,9 x 27,9 cm.
marzo 2021
Seis números para tres circunferencias II
Coloca los divisores de 12: 1, 2, 3, 4, 6 y 12, en los seis círculos azules, sin repetir ninguno, de forma que el producto de los números colocados en las tres circunferencias rojas sea el mismo.
(Haciendo «click» sobre la imagen puedes practicar con el juego realizado en GeoGebra).
Seis números para tres circunferencias I
Coloca los números 1, 2, 3, 4, 5 y 6 en los seis círculos rojos, sin repetir ninguno, de forma que la suma de los números colocados en las tres circunferencias azules sea la misma.
(Haciendo «click» sobre la imagen puedes practicar con el juego realizado en GeoGebra).
Círculos inscritos
En un cuadrado de lado «l» se inscriben círculos según se observa en la figura.
• ¿Cuál es la sucesión del número de círculos que se pueden inscribir?
• Calcula el término general de la sucesión que forman la suma de las áreas de los círculos.
Polígonos estrellados y estrellas en un heptágono regular
Un polígono regular estrellado se obtiene uniendo los vértices de un polígono regular de forma no consecutiva, empezando y acabando por el mismo y pasando solamente una vez por los demás.
En en un heptágono regular se pueden construir dos polígonos regulares estrellados.
• Uniendo dos vértices dejando un vértice intermedio entre ellos.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
• Uniendo dos vértices dejando dos vértices intermedios entre ellos.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
Universo matemático. Capítulo 10.
La búsqueda de un sueño, orden en el caos.
La serie “Universo matemático” fue creada por el profesor Antonio Pérez Sanz y producida por RTVE en 2000. Ahora RTVE la pone a disposición de los docentes a través de su menú “a la carta”.
Haz click sobre la imagen inferior para verlo.
División de un segmento en la proporción áurea
División de un segmento, con regla y compás, en dos segmentos cuya razón es el número de oro.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
El número de oro
Su descubrimiento se remonta al siglo V a. C., en la época de la Grecia Clásica, en la que era muy utilizado en arquitectura y escultura. Sin embargo hubo que esperar hasta el siglo XIX para conocerlo por la sexta letra del abecedario griego “Φ”, inicial del nombre del escultor griego Fidias (490-431 a.C.) que lo utilizó en sus obras.
Euclides (325-265 a.C.), en el siglo III a.C. lo utiliza en sus Elementos. En el año 1500 Luca Pacioli (1447-1517) lo reconocía como La divina Proporción. El nombre de Número de Oro o Proporción Áurea se le da en es siglo XIX en Alemania.
Posiblemente su descubrimiento se debe al estudio de las proporciones y de la medida de un segmento. Vamos a dividir un segmento de longitud una unidad en dos partes, de forma que la razón entre la parte mayor y la parte menor sea igual a la razón entre el total y la parte mayor. A esta forma de dividir un segmento se le conoce como proporción o sección áurea.
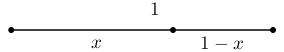
De la proporción deseada resulta la ecuación de segundo grado:
De las dos soluciones de la ecuación, solo será válida la solución positiva. Las medidas de las dos partes en que queda dividido el segmento, «x» y «1-x», son:
El número de oro, Φ, es la razón entre la parte mayor y la menor:
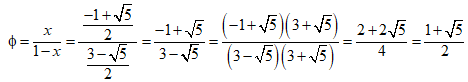
El número de oro es un número irracional, es decir, está formado por infinitas cifras decimales no periódicas. Hoy en día, es fácil calcular el número de oro con una gran cantidad de cifras decimales utilizando un ordenador.
Φ=1.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748 …
Ternas pitagóricas
Una terna pitagórica es un grupo de tres números naturales a, b y c que verifican: a2=b2+c2. Es decir, tres números naturales que pueden ser las medidas de los lados de un triángulo rectángulo y que, por tanto, verifican el Teorema de Pitágoras.
Es muy conocida la terna pitagórica formada por los números 5, 4 y 3, e incluso la formada por 13, 12 y 5. También que los múltiplos de una terna pitagórica también forman una terna pitagórica. Pero, ¿cuántas ternas pitagóricas existen? La siguiente aplicación muestra el procedimiento para construirlas.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y construir ternas pitagóricas.
Galileo Galilei
«Si comenzase de nuevo mis estudios, seguiría el consejo de Platón y comenzaría con las Matemáticas».
Galileo Galilei.
Pisa, 15 de febrero de 1564 – Arcetri, 8 de enero de 1642.
Astrónomo italiano, con mucho interés por todas las ciencias. Inventó el telescopio y realizó descubrimientos de objetos celestes. Defendió la teoría del heliocentrismo.
