Interpretación de un gráfico estadístico
Otro punto de vista de un gráfico estadístico
abril 2021
Triángulo de Penrose
Aunque lleva el nombre de triángulo de Penrose, debido al físico Roger Penrose, (1931- ), que lo popularizó, fue creado por el artista sueco Oscar Reutersvärd, (1915-2002), en el año 1934.
Más por menos. Capítulo 2
Movimientos en el plano.
Las matemáticas están más cerca de todos nosotros de lo que pensamos. ‘Más por menos’ ofrece explicaciones sencillas y didácticas sobre conceptos matemáticos y su correspondencia con la realidad, sin ser necesaria una formación previa para entender los conceptos explicados. Esta serie consta de trece capítulos y fue emitida por rtve en el programa «La aventura del saber».
Haz click sobre la imagen inferior para verlo.
Cálculos infinitos con resultado finito
Con algo de ingenio, calcula el resultado final de las dos operaciones.
 |
 |
Cuadrados y triángulos
← ¿Cuántos cuadrados hay en esta figura?
¿Y cuántos triángulos hay en esta otra? →
Cuadrado mágico «Virgen del Calvario» de Zurgena
Zurgena es un pequeño pueblo de la provincia de Almería. En un lateral exterior de su Ermita de la «Virgen del Calvario», después de unas obras de reforma que se iniciaron en el año 1992, figura un interesante cuadrado mágico de orden 7.
Este cuadrado mágico contiene los 49 primeros números naturales y está formado por:
• Un cuadrado mágico de orden 3, de constante mágica 75, que contiene los números desde el 21 hasta el 29. Los números de las tres filas, las tres columnas y las dos diagonales suman 75.
La constante mágica de un cuadrado mágico de orden 3 se calcula sumando todos los números utilizados y dividiendo la suma por 3.
• Un cuadrado mágico de orden 5, de constante mágica 125, que contiene en su interior el cuadrado mágico de orden 3 y, en las filas y columnas exteriores, los números desde el 13 hasta el 20 y desde el 30 hasta el 37. Los números de las cinco filas, las cinco columnas y las dos diagonales suman 125.
La constante mágica de un cuadrado mágico de orden 5 se calcula sumando todos los números utilizados y dividiendo la suma por 5.
• Un cuadrado mágico de orden 7, de constante mágica 175, que contiene en su interior, el cuadrado mágico de orden 5 y, en las filas y columnas exteriores, los números desde el 1 hasta el 12 y desde el 38 hasta el 49. Los números de las siete filas, las siete columnas y las dos diagonales suman 175.
La constante mágica de un cuadrado mágico de orden 7 se calcula sumando todos los números utilizados y dividiendo la suma por 7.
Además el cuadrado mágico presenta otras curiosidades:
→ La suma de los números situados en las casillas exteriores del cuadrado de orden 3 es 200, las del cuadrado de orden 5 es 400 y las del cuadrado de orden 7 es 600.
Con los 49 primeros números naturales se pueden formar 24 parejas de números que suman 50. Estas parejas están situadas en el cuadrado de forma simétrica respecto de los ejes de simetría horizontal o vertical, o respecto de la casilla central. Esto supone que se puedan combinar en grupos de números cuya suma sea un múltiplo de 50 y que formen en el cuadrado configuraciones simétricas.
→ Si se combinan dos de estas parejas, se obtienen grupos de cuatro números cuya suma es 100. Si se le añade la casilla central, la suma sería 125. A continuación se indican algunos más representativos:
En el cuadrado mágico de orden 3:
En el cuadrado mágico de orden 5:
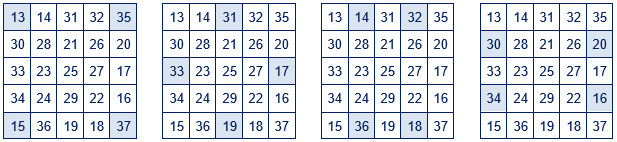
En el cuadrado mágico de orden 7:
→ Si se combinan cuatro de estas parejas, se obtienen grupos de ocho números cuya suma es 200. Si se le añade la casilla central, la suma sería 225. Algunos de ellos:
→ Si se combinan seis de estas parejas, se obtienen grupos de doce números cuya suma es 300. Si se le añade la casilla central, la suma sería 325. Algunos de ellos:
→ Si se combinan ocho de estas parejas, se obtienen grupos de dieciséis números cuya suma es 400. Si se le añade la casilla central, la suma sería 425. Algunos de ellos:
Y de esta forma se podría continuar obteniendo interesantes configuraciones.
Mi felicitación a su autor, Antonio Jiménez Jiménez, por este extraordinario cuadrado mágico y mi agradecimiento por su amabilidad y por la información recibida para poder elaborar esta entrada del blog.
Polígonos estrellados y estrellas en un eneágono regular
Un polígono regular estrellado se obtiene uniendo los vértices de un polígono regular de forma no consecutiva, empezando y acabando por el mismo y pasando solamente una vez por los demás.
En en un eneágono regular se pueden construir dos polígonos regulares estrellados y tres estrellas.
• Uniendo dos vértices dejando un vértice intermedio entre ellos se obtiene un polígono regular estrellado.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
• Uniendo dos vértices dejando dos vértices intermedios entre ellos no se puede construir un polígono regular estrellado, se obtienen tres triángulos equiláteros. Pero sí se puede construir una estrella con los tres triángulos.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
• Uniendo dos vértices dejando tres vértices intermedios entre ellos sí se obtiene un polígono regular estrellado.
Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.
El número de oro es un número algebraico
El número de oro es un número algebraico. Esto significa que:
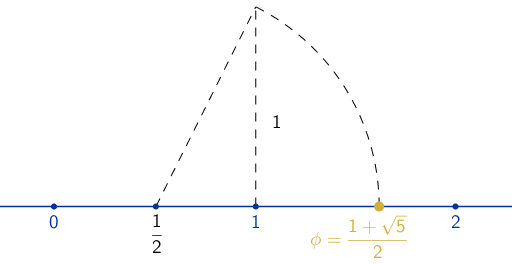
• Se puede representar gráficamente con regla y compás. Para representar el número de oro con regla y compás se sigue una construcción similar a la realizada para construir el rectángulo de oro:
Se traza un segmento de longitud 1, perpendicular a la recta real por el 1.
Con centro en 1/2 se traza un arco de circunferencia que pasa por el extremo del segmento anterior.
Este arco corta a la recta real en el número de oro.
• Se obtiene como solución de una ecuación polinómica con coeficientes racionales. El número de oro es una de las soluciones de la ecuación:
Tres esferas II
M.C. Escher. Tres esferas II. 1946.
Litografía. 46,3 x 26,9 cm.
El número 55
En una entrada anterior aparece un resultado y su demostración de que todos los números naturales son interesantes en Matemáticas. Uno de los números con un interés especial es el número 55 porque aparece en estas tres sucesiones importantes:
| • Es el décimo número triangular: | • Es el quinto número piramidal cuadrangular: |
| 1 , 3 , 6 , 10 , 15 , 21, 28 , 36 , 45 , 55 , … | 1 , 5 , 14 , 30 , 55 , 91, 140 , 204 , 285 , 385 , … |
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 =55 |
12 + 22 + 32 + 42 + 52 = 55 |
• Es es décimo número de la sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, . . .
1+1=2 , 1+2=3 , 2+3=5 , 3+5=8 , 5+8=13 , 8+13=21 , 13+21=34 , 21+34=55
