En la fachada de entrada al I.E.S. José de Mora de Baza, Granada, hay tres cuadrados mágicos multiplicativos, desde el jueves 3 de marzo de 2022.

Los cuadrados están construidos utilizando todos los divisores de números que se pueden expresar como potencias de 6. En la parte inferior de cada uno de ellos se indica la constante mágica, también es una potencia de 6.

• El primero de ellos, de orden 3, está construido con los divisores de 36=6² y tiene constante mágica 6³. Ya existía con anterioridad, pero es el origen del estudio y generalización que da lugar a los otros dos.

• El segundo, de orden 4, está construido con los divisores de 216=6³ y tiene constante mágica 6⁶=46656. Tiene todas las propiedades del cuadrado mágico aditivo conocido como Chautisa Yantra.

• El tercero, de orden 5, está construido con los divisores de 1296=6⁴ y tiene constante mágica 6¹⁰=60466176. Contiene en su interior un cuadrado mágico multiplicativo de orden 3, de constante mágica 6⁶=46656.

Estos dos cuadrados mágicos han sido construidos, en el año 2021, por el profesor de Matemáticas, Luis Barrios Calmaestra.

Los mosaicos han sido realizados por el alumnado de primer curso de Bachillerato de Artes, trabajo facilitado por el profesor de Artes, Ángel Montero. Se han utilizado baldosas de terracota pigmentadas y vidriadas, sometidas a una cocción de 980º.

Cuadrado mágico multiplicativo de orden 3

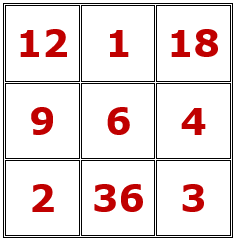
Con los nueve divisores del número 36=2²·3²=6²: 1, 2, 3, 4, 6, 9, 12, 18 y 36, se puede construir el siguiente cuadrado mágico multiplicativo de orden 3, de constante mágica 216=2³·3³=6³.

• El producto de los números situados en cada fila es igual a 216=6³.

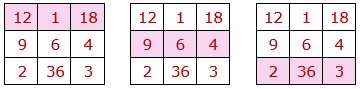
• El producto de los números situados en cada columna es igual a 216=6³.

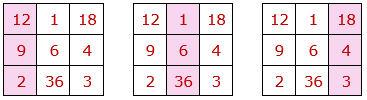
• El producto de los números situados en cada diagonal es igual a 216=6³.

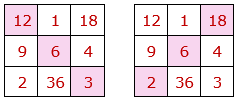
• El producto de los siguientes grupos de cuatro números es 1296=6⁴.

Al realizar giros o simetrías en el cuadrado se obtiene otro cuadrado mágico con las mismas características.

Cuadrado mágico multiplicativo de orden 4

Con los dieciséis divisores del número 216=2³·3³=6³: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108 y 216, se puede construir el siguiente cuadrado mágico multiplicativo de orden 4, de constante mágica 46656=2⁶·3⁶=6⁶.

• El producto de los números situados en cada fila es igual a 46656=6⁶.

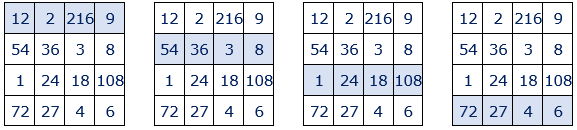
• El producto de los números situados en cada columna es igual a 46656=6⁶.

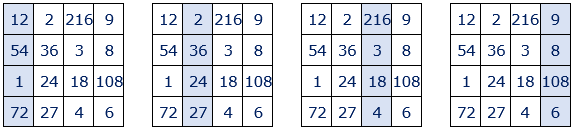
• El producto de los números situados en cada diagonal es igual a 46656=6⁶.

• El producto de los cuatro números situados en las esquinas es igual a 46656=6⁶. También el producto de los números situados en los cuatro cuadrados centrales.

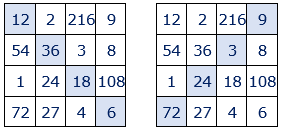
• El producto de los cuatro números situados en cada uno de los nueve cuadrados de 2×2 que se pueden formar es igual a 46656=6⁶.

• El producto de los números situados en las esquinas de los cuadrados de 3×3 es igual a 46656=6⁶.

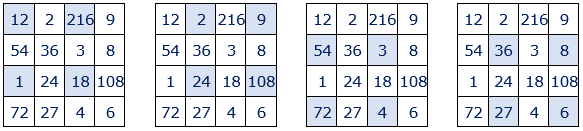
• El producto de los números situados en las diagonales secundarias es igual a 46656=6⁶.

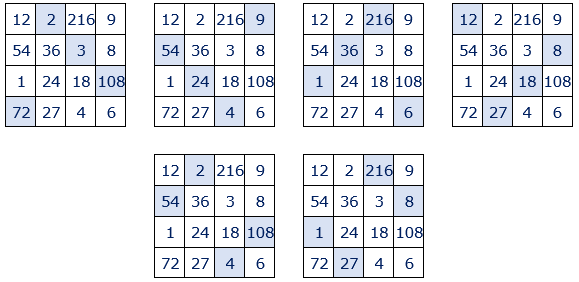
• Otros grupos de cuatro números cuyo producto es igual a 46656=6⁶.

• Los dos primeros números del cuadrado son 12 y 2. Las letras del abecedario que ocupan los lugares 12º, «L» y 2º, «B», corresponden a las iniciales del autor.

Al realizar giros o simetrías en el cuadrado se obtiene otro cuadrado mágico con las mismas características.

Cuadrado mágico multiplicativo de orden 5

Con los veinticinco divisores del número 1296=2⁴·3⁴=6⁴: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 36, 48, 54, 72, 81, 108, 144, 162, 216, 324, 432, 648 y 1296, se puede construir el siguiente cuadrado mágico multiplicativo de orden 5, de constante mágica 60466176=2¹⁰·3¹⁰=6¹⁰.

El cuadrado interior es un cuadrado mágico multiplicativo de orden 3 y de constante mágica 46656=2⁶·3⁶=6⁶.

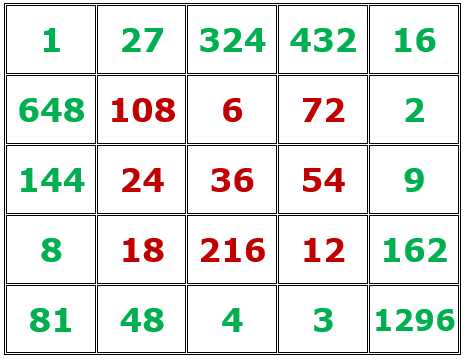
• El cuadrado interior es un cuadrado mágico multiplicativo de orden 3. El producto de los números situados en las tres filas, en las tres columnas y en las dos diagonales principales es 46656=2⁶·3⁶=6⁶.

• El cuadrado completo es un cuadrado mágico multiplicativo de orden 5. El producto de los números situados en las cinco filas, en las cinco columnas y en las dos diagonales principales es 60466176=2¹⁰·3¹⁰=6¹⁰.

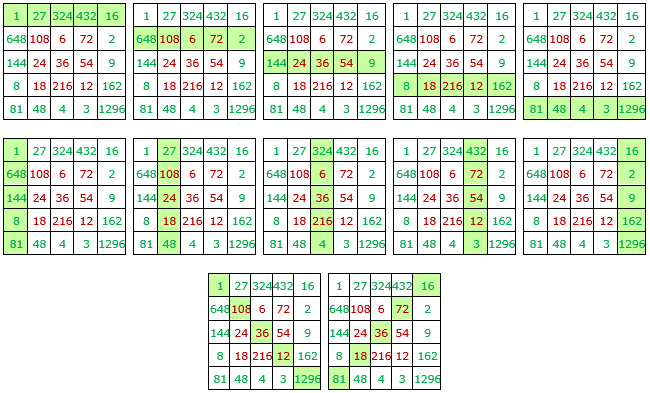
Y además:

• Algunos grupos de cuatro números cuyo producto es 6⁸, con la casilla central, 6¹⁰.

• Algunos grupos de ocho números cuyo producto es 6¹⁶, con la casilla central, 6¹⁸.

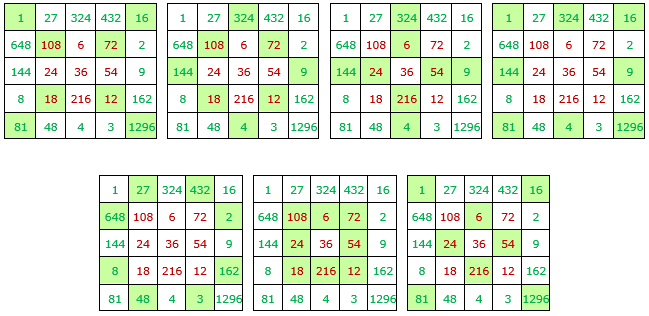
• Algunos grupos de doce números cuyo producto es 6²⁴, con la casilla central, 6²⁶.

• Algunos grupos de dieciséis números cuyo producto es 6³², con la casilla central, 6³⁴.

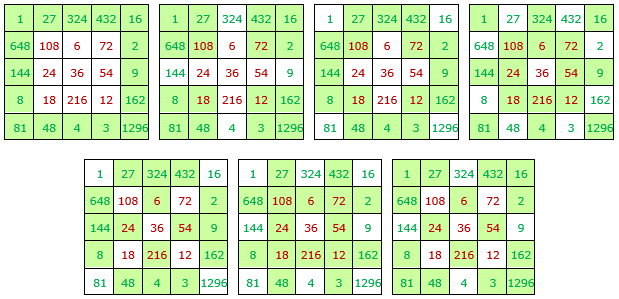
Al realizar giros o simetrías en el cuadrado se obtiene otro cuadrado mágico con las mismas características.