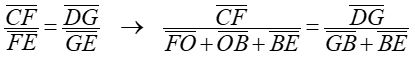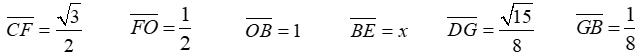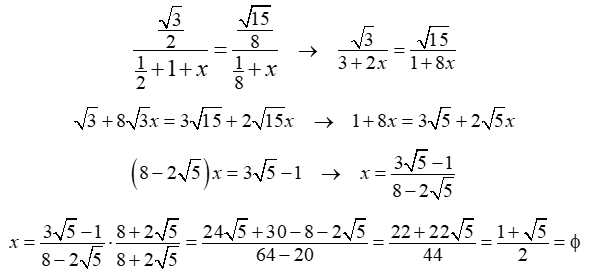Construcciones geométricas

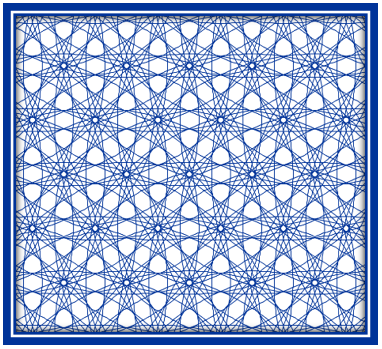
La pajarita nazarí es el mosaico más representativo de la Alhambra. Ya se le ha dedicado dos entradas anteriores en este blog. Una en la que aparece su construcción y otra en la que se modifica su aspecto. En esta tercera entrada se va a modificar su tamaño en un mosaico y se muestra el efecto que produce.

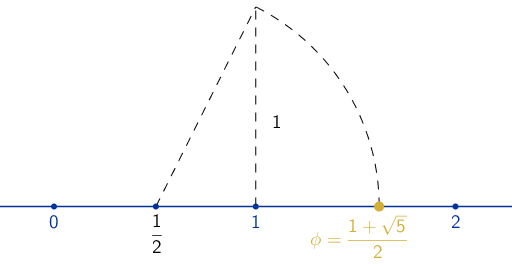
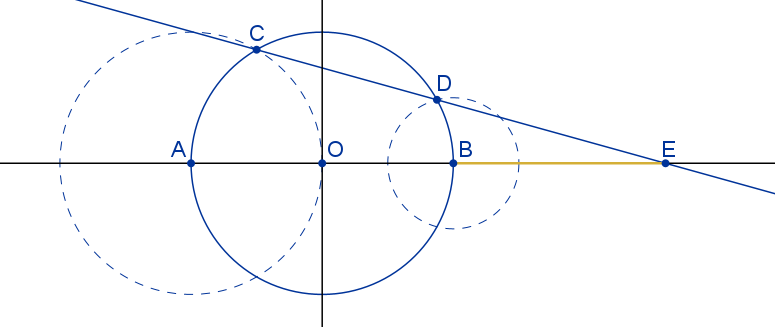
En la entrada «pajarita nazarí»  de este blog, se estudió como se obtiene esta figura a partir de un triángulo equilátero.

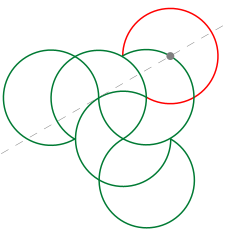
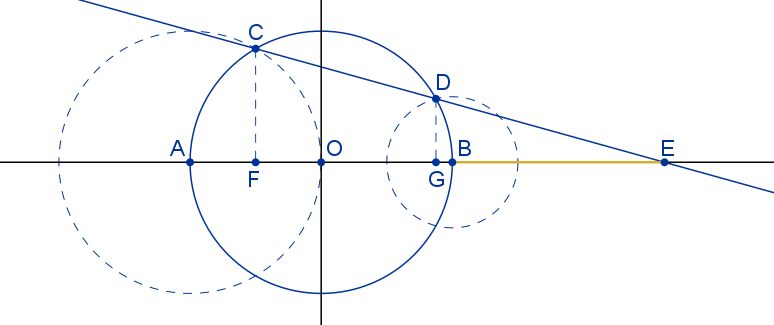
Posteriormente, en la entrada «Pajaritas animadas«, se estudió la existencia de otras pajaritas, distintas de la nazarí, modificando la posición del centro de sus arcos y, por tanto, también el radio de los mismos. En algunos casos la pajarita se aproxima al triángulo equilátero de la que se obtiene y, en otros, la pajarita se deforma dando lugar a construcciones geométricas sorprendentes. La siguiente imagen se obtiene a partir de un mosaico con pajaritas.

Otra entrada de este blog lleva el título de «Arte Geométrico«. En esta entrada no aparece la pajarita nazarí. Se estudia el comportamiento de distintos mosaicos con circunferencias y polígonos regulares, cuando se mantienen fijos sus centros y van aumentando su tamaño intersecando sus lados, obteniéndose maravillosas construcciones geométricas, que en algunos casos se pueden considerar auténticas obras de arte geométrico.

Y en esta entrada, Arte geométrico con la pajarita nazarí, se utiliza el procedimiento anterior para construir a partir de un mosaico de pajaritas nazaríes, dejando fijos los centros y aumentando el tamaño de las pajaritas, otras estructuras geométricas extraordinarias como se puede comprobar en las siguientes actividades.

Haz «click» sobre cualquiera de las siguientes imágenes para observar estos gráficos.

En las construcciones a las que se accede:

· Se puede activar o desactivar la animación automática con los botones que aparecen en la esquina inferior izquierda.

· Se puede modificar la construcción manualmente, seleccionando y moviendo con el ratón el deslizador (punto que aparece en un segmento en la parte inferior central) .

· En cualquier momento, se puede acercar o alejar la construcción pulsando sobre los botones de «Zoom».

• En este primer caso se muestra una situación con seis pajaritas nada más, para comprender mejor como se comportan al dejar fijos sus centros y modificar su tamaño.

• En este segundo caso se utiliza un mosaico de pajaritas, aunque incompleto. Como se puede apreciar en la primera imagen solamente aparecen las pajaritas que se encuentran en la posición de la figura inicial. 

• Y en este tercer y último caso se utiliza un mosaico de pajaritas completo, obteniéndose una estructura geométrica todavía más compleja que la anterior. 

La pajarita nazarí es, posiblemente, la figura más interesante y conocida de los mosaicos de la Alhambra. En algunos de los mosaicos aparece como una figura compacta y en otros aparece con hexágonos o estrellas en su interior. 

El mosaico se construye a partir del recubrimiento del plano con triángulos equiláteros. En la figura siguiente se puede observar como se obtiene la pajarita de un triángulo equilátero. Si se divide el triángulo equilátero en cuatro triángulos equiláteros iguales, los centros de los arcos exteriores son los baricentros de tres de estos triángulos.

Haz «click» sobre la imagen para abrir una entrada anterior de este blog y comprobar la construcción de la pajarita nazarí con una escena del Proyecto Descartes y con GeoGebra.

Aunque esta es la forma de construir la pajarita original, se pueden construir otras pajaritas, con menor o mayor curvatura de sus arcos, modificando la posición del centro de cada uno de ellos. Estos centros siempre deben estar en la mediatriz del segmento que une cada uno de los vértices con los puntos medios de los lados.

Haz «click» sobre cualquiera de las siguientes imágenes para observar como cambia la pajarita al moverse los centros por cada una de las mediatrices. Se representa solamente un centro (del arco de color rojo) y una mediatriz para ver la construcción con mayor claridad. Observa qué sucede cuando las coordenadas del centro que se muestra toman valores muy grandes.

Si en lugar de una sola pajarita, utilizamos un grupo de pajaritas, en este caso formando hexágonos, cuando las coordenadas del centro que se representa toman valores cada vez mayores, se obtienen gráficos  sorprendentes y muy interesantes. 

Haz «click» sobre cualquiera de las siguientes imágenes para observar estos gráficos.

En la construcción que se abre, también en el caso anterior y en el siguiente:

• Se puede activar o desactivar la animación automática con los botones que aparecen en la esquina inferior izquierda.

• Se puede modificar la construcción manualmente, seleccionando y moviendo con el ratón el punto gris (centro de uno de los arcos) por la recta discontinua .

• En cualquier momento, se puede acercar o alejar la construcción pulsando sobre los botones de «Zoom».

• En este caso particular, se puede cambiar la construcción modificando la variable «lado» con el deslizador de la parte inferior derecha.

Y haciendo «click» ahora sobre alguna de estas imágenes se pueden observar los gráficos que se obtienen en un mosaico de pajaritas completo.