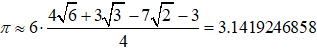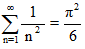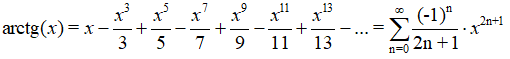El número de cifras decimales del número π conocidas actualmente es de 62’8 billones. Con mayor exactitud son exactamente:

62.831.853.071.796

Esta cantidad ha sido calculada por Científicos del Centro de Análisis de Datos, Visualización y Simulación de la Universidad de Ciencias Aplicadas de Graubünden (FHGR), Suiza.

Sin embargo, con 15 cifras decimales es suficiente para realizar cálculos exactos.

DÍA INTERNACIONAL DE LAS MATEMÁTICAS. DÍA DE π.

Y después del esfuerzo de todas las personas que, durante cuarenta siglos, han contribuido en primer lugar en el descubrimiento de π y después en el cálculo de cada vez más cifras decimales, hasta llegar a 31.4 billones, a continuación se expone el siguiente razonamiento que, de ser cierto, haría inútil todo ese esfuerzo y trabajo.

Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.

Según esto:

¿Se puede deducir que π=2? ¿Se puede deducir que π es racional? ¿Se puede deducir que π no es trascendente?

Sabiendo que la longitud de una circunferencia se calcula con la fórmula: L=2πr y que el área del círculo se obtiene con la fórmula A=πr², realiza mentalmente las siguientes actividades dando el resultado en función del número π:

     Actividad 1.

a) Calcula la longitud de la circunferencia cuando r = 1 cm.

b) Calcula el área del círculo cuando r = 1 cm.

     Actividad 2.

a) Calcula la longitud de la circunferencia cuando r = π cm.

b) Calcula el área del círculo cuando r = π cm.

     Actividad 3.

a) Calcula la longitud de la circunferencia cuando r = π² cm.

b) Calcula el área del círculo cuando r = π² cm.

     Actividad 4.

a) Calcula la longitud de la circunferencia cuando r = 1/π cm.

b) Calcula el área del círculo cuando r = 1/π cm.

     Actividad 5.

a) ¿Cuál es el valor de r para que la longitud de la circunferencia sea 1 cm?

b) ¿Cuál es el valor de r para que el área del círculo sea 1 cm²?

     Actividad 6.

a) ¿Cuál es el valor de r para que la longitud de la circunferencia sea π cm?

b) ¿Cuál es el valor de r para que el área del círculo sea π cm²?

     Actividad 7.

a) ¿Cuál es el valor de r para que la longitud de la circunferencia sea π² cm?

b) ¿Cuál es el valor de r para que el área del círculo sea π² cm²?

     Actividad 8.

a) ¿Para qué valor de r coinciden la longitud y el área?

b) ¿Para qué valor de r la longitud de la circunferencia es el doble del área del círculo?

c) ¿Para qué valor de r el área del círculo es el doble de la longitud de la circunferencia?

     Actividad 9.

a) ¿Cuál debe ser la longitud del lado de un cuadrado para que tenga la misma superficie que una circunferencia de radio r?

b) ¿Cuál debe ser la longitud del radio de una circunferencia para que tenga la misma superficie que un cuadrado de lado l?

La informática y la utilización de ordenadores cada vez más potentes y rápidos, han hecho posible el cálculo de cada vez más cifras decimales del número π y en menos tiempo. Para ello se han utilizado, en primer lugar, fórmulas del tipo arcotangente y posteriormente se han necesitado fórmulas más potentes.

Una de ellas fue la descubierta en 1914 por el matemático indio Ramanujan (1887-1920):

Esta fórmula fue utilizada para obtener 17526200 decimales en 1985.

Y otra fórmula descubierta por los hermanos Chudnosky, David (1947-) y Gregory (1952-):

Fue usada por los hermanos Chudnovsky para calcular más de mil millones de dígitos. Se utilizó en el cálculo de 2.7 billones de dígitos en diciembre de 2009, 5 billones de dígitos en agosto de 2010, y 10 billones de dígitos en octubre de 2011.

Actualmente se conocen 31.4 billones de cifras decimales del número π, récord conseguido en 2019 por la informática japonesa Emma Haruka Iwao (1986,-).

Aunque se insista en la búsqueda de cada vez más cifras decimales, para los cálculos astronómicos o microscópicos que se puedan realizar, es suficiente con no más de 40 cifras decimales.

Las 40 primeras cifras decimales del número π son:

    π ≈ 3.1415926535897932384626433832795028841971

El número π es un número trascendente, esto significa que no se puede representar con regla y compás. Sin embargo, algunos matemáticos han intentado conseguir alguna aproximación gráfica. El matemático italiano Lorenzo Mascheroni (1750-1800), realizó una aproximación geométrica del número π, en la que se obtiene: 

Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.

El número π es un número trascendente, esto significa que no se puede representar con regla y compás. Sin embargo, algunos matemáticos han intentado conseguir alguna aproximación gráfica. El matemático polaco Adam Kochanski (1631-1700), realizó algunas aproximaciones geométricas del número π, intentando resolver el problema de la cuadratura del círculo, obteniendo: 

Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.

El número π es un número trascendente, esto significa que no se puede representar con regla y compás. Sin embargo, algunos matemáticos han intentado conseguir alguna aproximación gráfica. El filósofo inglés Thomas Hobbes (1588-1679), intentando resolver el problema de la cuadratura del círculo, obtuvo como aproximación. 

Haz «click» sobre la imagen para abrir la construcción con GeoGebra y seguirla paso a paso.

El profesor de astronomía inglés John Machin, (1680-1751), encuentra un nuevo método para calcular aproximaciones de π, utilizando también el desarrollo en serie de la arcotangente. En 1706, consiguió 100 decimales calculados a mano con la fórmula:

El matemático suizo Leonhard Euler, (1707-1783), en 1764, calculó en una hora veinte cifras decimales del número π con la fórmula:

El matemático alemán Karl Friedrich Gauss, (1777-1855), también descubrió algunas fórmulas del mismo tipo. Una de las más utilizadas ha sido:

El matemático inglés William Shanks, (1812-1882), dedicó veinte años al cálculo de cifras decimales de π y obtuvo en 1853, 707 decimales, con la fórmula de Machin. Sin embargo, cometió un error en el decimal que ocupaba el lugar 528º y a partir de él, todos los demás estaban mal calculados.

El matemático suizo Leonhard Euler (1707-1783), en 1734, consiguió calcular la suma de los inversos de los cuadrados de los números naturales, obteniendo:

Utilizando el emulador de la calculadora Classwiz fx-570SP X Iberia, podemos obtener el valor de la suma para 10, 100, 1000, 10000, 100000 y 1000000 de sumandos y, posteriormente la aproximación de π:

A partir del desarrollo en serie de «arctg x» del inglés James Gregory:

El matemático alemán Gottfried Wilheim von Leibniz (1646-1716), obtiene en 1674, para x=1:

Utilizando el emulador de la calculadora Classwiz fx-570SP X Iberia, podemos obtener el valor de la suma para 10, 100, 1000, 10000, 100000 y 1000000 de sumandos: