Números curiosos de tres cifras VII
Calcula todos los números naturales de tres cifras, abc, que verifican que la suma del primero y el segundo es igual al cociente entre el tercero y el primero:
Adicción Matemática Blog
figuras con arcos V
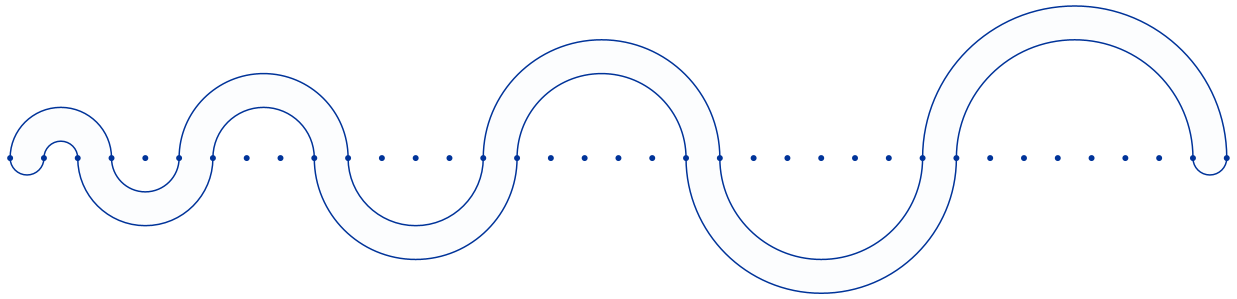
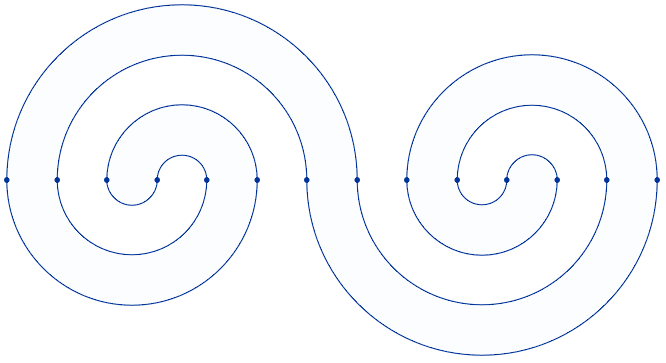
Sabiendo que la distancia entre dos puntos consecutivos es de 1 centímetro, calcula la superficie y el perímetro de la región coloreada. Expresa la solución utilizando el número π y fracciones, sin utilizar números decimales.
Números curiosos de tres cifras VI
Calcula todos los números naturales de tres cifras, abc, que verifican que la suma del primero y el segundo es igual al cociente entre el primero y el tercero:
Figuras con arcos IV
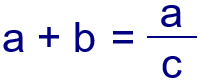
Sabiendo que la distancia entre dos puntos consecutivos es de 1 centímetro, calcula la superficie y el perímetro de la región coloreada. Expresa la solución utilizando el número π y fracciones, sin utilizar números decimales.
Números curiosos de tres cifras V
Calcula todos los números naturales de tres cifras, abc, que verifican que la suma del primero y el segundo es igual al producto del segundo y el tercero:
a + b = b × c
Arte geométrico
Esta miscelánea del Proyecto Descartes recrea la visita a un museo de arte geométrico. En tan solo ocho salas dedicadas a la circunferencia y a siete polígonos regulares, utilizando pulsadores, el visitante puede contemplar hasta 17000 construcciones geométricas, algunas de ellas son verdaderas obras de arte geométrico. Además tiene la posibilidad de acercar o alejar la construcción para observar de cerca algunos detalles o tener una visión global de la estructura geométrica.
En cualquier mosaico geométrico, por básico que pueda parecer, se puede admirar la belleza de su construcción y como los elementos geométricos que lo componen se distribuyen, mediante traslaciones giros y simetrías, proporcionándole equilibrio y armonía.
Cuando estos elementos cobran movimiento, con ayuda de la tecnología, en este caso con el Proyecto Descartes, el mosaico describe extraordinarias estructuras geométricas que aumentan su complejidad a medida que aumenta el número de lados de los polígonos regulares y que pueden ser consideradas como auténticas obras de arte.
Haz «click» sobre cualquiera de las imágenes para abrir la miscelánea del Proyecto Descartes.
Calendario Matemático SEMCV «Al Khwarizmi». 2024-25. Marzo
La Sociedad de Educación Matemática de la Comunidad Valenciana «Al Khwarizmi» publica la séptima página de su Calendario Matemático anual, correspondiente al mes de marzo del curso 2024-25. Los problemas de los días 1 y 28-29 corresponden a actividades de este blog.
Se puede acceder a la publicación haciendo «click» sobre la imagen siguiente.
Johannes Kepler
«Donde hay materia, hay geometría».
Johannes Kepler.
Weil der Stadt, 27 de diciembre de 1571 – Ratisbona, 15 de noviembre de 1630.
Astrónomo y matemático alemán.
Es conocido por las leyes del movimiento de los planetas alrededor del Sol.
Sucesión de cuadrados III
• Se dividen los lados de cuatro cuadrados de 1 cm2 de superficie en 5 partes iguales. En cada uno de ellos, se une cada uno de los vértices con la primera, segunda, tercera y cuarta divisiones respectivamente, de uno de los lados no contiguos, según se observa en la figura, formando cuadrados interiores más pequeños. Deduce una fórmula para el cálculo de la superficie de cada uno de estos cuadrados, según la división elegida.
• Deduce una fórmula, en función de m y n, para el área del cuadrado interior si se divide el lado del cuadrado en n partes iguales y se une cada vértice con la división que ocupa el lugar m de uno de los lados no contiguos.
Números curiosos de cuatro cifras X
Calcula todos los números naturales de cuatro cifras, abcd, que verifican que el cuadrado de la última cifra es igual a la suma de las tres primeras:
a + b + c = d2
