Números de cinco cifras
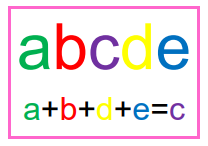
¿Cuántos números de cinco cifras distintas verifican que la suma de las centenas es igual a la suma de las restantes cifras.
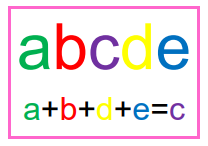
¿Cuántos números de cinco cifras distintas verifican que la suma de las centenas es igual a la suma de las restantes cifras.

En el cuadrado de la figura, de 4 cm de lado, se traza el segmento EF que lo divide en dos cuadriláteros iguales, ABFE y CDEF. Sabiendo que el perímetro de cualquiera de los cuadriláteros es 13 cm, calcula la longitud del segmento BF.
El problema de la mascarilla.

Al colocar los números impares formando el siguiente triángulo, al sumar los números situados en cada fila se obtienen los cubos de los números naturales.

Se puede ampliar la información en el siguiente enlace:
Los números impares y las potencias de los números naturales.
Un número cuadrado perfecto es un número que se obtiene al elevar al cuadrado cualquier número natural. Se puede disponer formando cuadrados y se obtiene también como suma de números impares consecutivos.
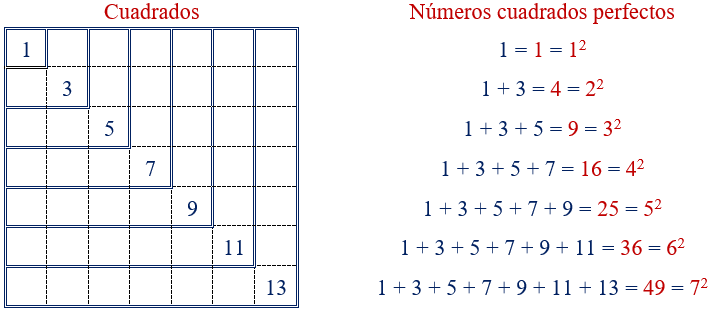
Los primeros números cuadrados perfectos son: 1 , 4 , 9 , 16 , 25 , 36 , 49 , 64 , 81 , 100 , …
La sucesión de números impares tiene como término general «an = 2n – 1«. Utilizando la suma de los elementos de una progresión aritmética, se obtiene la relación entre la suma de los números impares y los números cuadrados perfectos.
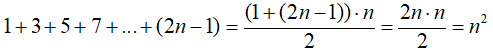
A partir de los vértices de un cuadrado (centros) se dibuja un arco de circunferencia de 90º de amplitud, con centro en uno de ellos y radio la longitud del lado del cuadrado. Posteriormente se continúa trazando arcos de 90º rotando los centros y utilizando el punto final del último arco como inicio del siguiente.
Haz «click» sobre la imagen para abrir la construcción de Geogebra.
Una calificación bien puesta.

Alberto Durero (1471-1528) es un artista renacentista alemán. Uno de sus grabados más famosos es «Melancolía I» que se encuentra en la Galería Nacional de arte de Karlsruhe (Alemania). En este grabado, realizado en 1514, hay algunos elementos matemáticos y, en la parte superior derecha, aparece un cuadrado mágico de orden cuatro.


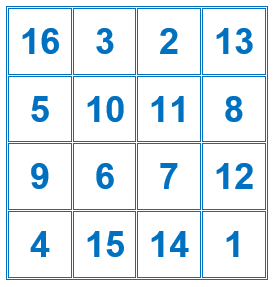
Es un cuadrado mágico construido con los dieciséis primeros números naturales, de constante mágica 34.
La suma de las cuatro filas es igual a 34.
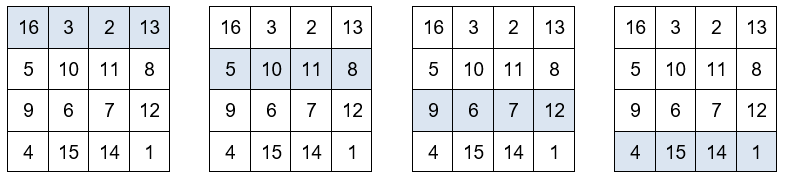
La suma de las cuatro columnas es igual a 34.
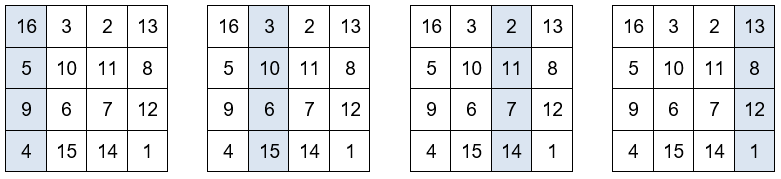
La suma de las dos diagonales es igual a 34.
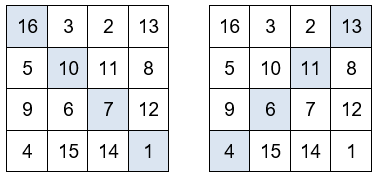
La suma de los cuatro números situados en las esquinas es igual a 34. También la suma de los números situados en los cuatro cuadrados centrales.
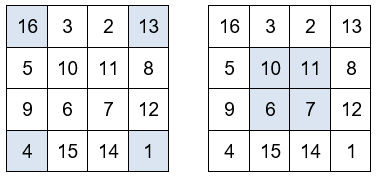
Si dividimos el cuadrado por la mitad de horizontal y verticalmente, se obtiene cuatro cuadrados con cuatro números cada uno. La suma de los números situados en cada uno de los cuadrados es igual a 34.
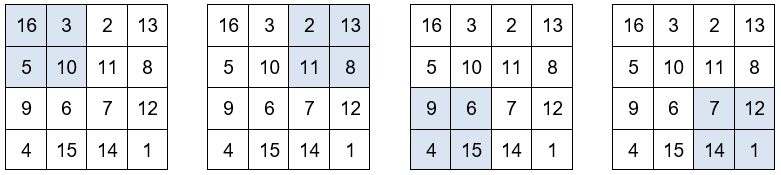
La suma los dos números centrales de la primera fila con los dos números centrales de la última es igual a 34. También la suma los dos números centrales de la primera columna con los dos números centrales de la última.
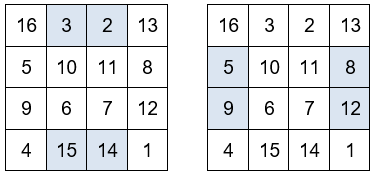
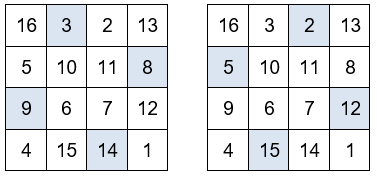
La suma de los números situados en las esquinas de los cuadrados de 3×3 es igual a 34.
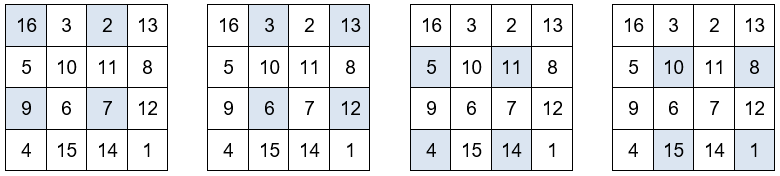
Otros grupos de números que también suman 34.
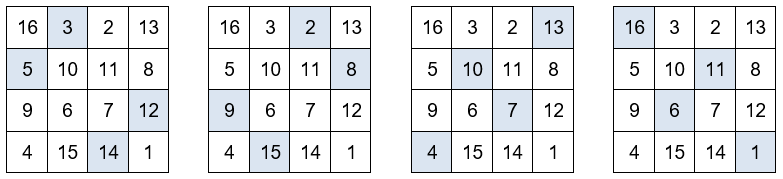

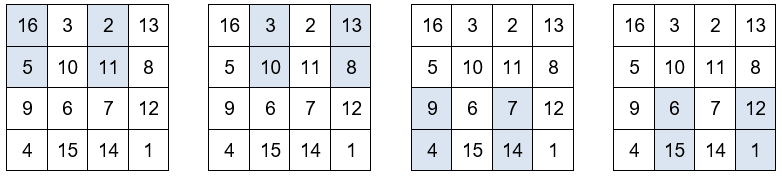


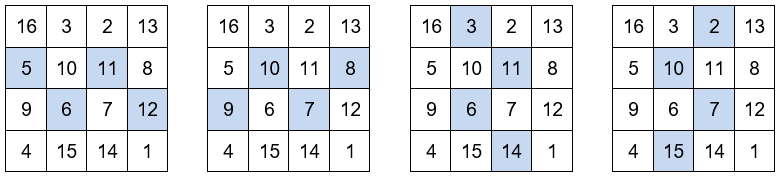
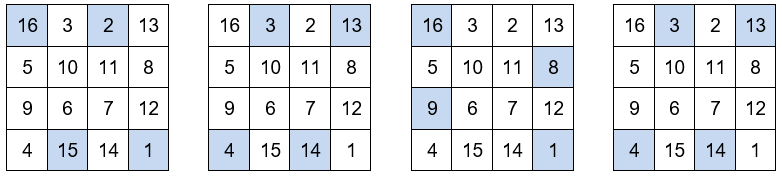

Y por último, en los dos cuadrados centrales de la última fila aparece el año de su realización, 1514. El primer número de la última fila, 4, corresponde al lugar que ocupa en el abecedario la inicial de su apellido, D. Y el último número de la última fila, 1, corresponde al lugar que ocupa en el abecedario la inicial de su nombre, A.