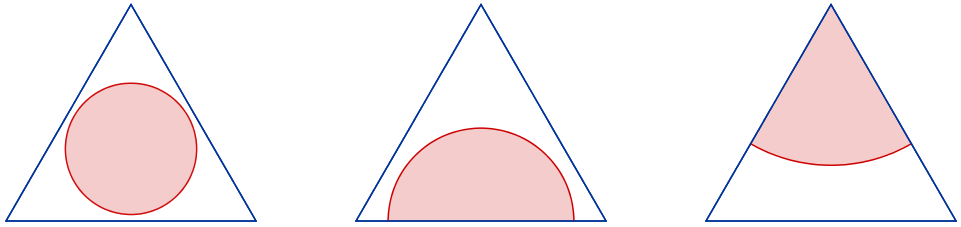
La mitad de la superficie de un triángulo
• ¿Qué radio debe tener un círculo, con centro en el baricentro de un triángulo equilátero, para que su superficie sea la mitad de la superficie del triángulo?
• ¿Qué radio debe tener un semicírculo, con centro en el punto medio del lado de un triángulo equilátero, para que su superficie sea la mitad de la superficie del triángulo?
• ¿Qué radio debe tener un sector circular de 60º, con centro en un vértice de un triángulo equilátero, para que su superficie sea la mitad de la superficie del triángulo?