Problemas con la suma
Estampida de vampiros en una clase de Matemáticas.
octubre 2022
Dos circunferencias tangentes
Las dos circunferencias de la figura son tangentes exteriores de radios r1 y r2 respectivamente. Se trazan radios perpendiculares a la recta que une los centros, que cortan a cada una de las circunferencias en los puntos A y B. Calcula la distancia entre estos dos puntos.
Si los radios son números naturales distintos, ¿puede ser la distancia entre A y B un número natural? En caso afirmativo, pon un ejemplo.
Godfrey Harold Hardy
«Un matemático, como un pintor o un poeta, es un fabricante de modelos. Si sus modelos son más duraderos que los de estos últimos, es debido a que están hechos de ideas. Los modelos del matemático, como los del pintor o los del poeta deben ser hermosos. La belleza es la primera prueba; no hay lugar permanente en el mundo para unas matemáticas feas».
Godfrey Harold Hardy.
Cranleigh, 7 de febrero de 1877 – Cambridge, 1 de diciembre de 1947.
Matemático británico.
Sucesión de Jacobsthal
La sucesión de Jacobsthal, debida al matemático alemán Ernst Jacobstal (1882-1965), es la siguiente sucesión de números:
0, 1, 1 , 3, 5, 11, 21, 43, 85, 171, 341, 683, 1365, 2731, 5461, . . .
• Esta sucesión se puede obtener como una sucesión recurrente conociendo los dos términos anteriores:
a1 = 0 , a2 = 1 , an = 2·an–2 + an–1
| a3=2a1+a2=0+1=1 | a4=2a2+a3=2+1=3 | a5=2a3+a4=2+3=5 | a6=2a4+a5=6+5=11 |
| a7=2a5+a6=10+11=21 | a8=2a6+a7=22+21=43 | a9=2a7+a8=42+43=85 | a10=2a8+a9=86+85=171 |
• Esta sucesión se puede obtener también como una sucesión recurrente conociendo el término anterior:
a1 = 0 , an = 2·an–1 +(-1)n
| a2=2a1+(-1)2=0+1=1 | a3=2a2+(-1)3=2–1=1 | a4=2a3+(-1)4=2+1=3 | a5=2a4+(-1)5=6–1=5 |
| a6=2a5+(-1)6=10+1=11 | a7=2a6+(-1)7=22–1=21 | a8=2a7+(-1)8=42+1=43 | a9=2a8+(-1)9=86–1=85 |
• También se puede obtener cualquier término de la sucesión sin necesidad de conocer ninguno de los términos anteriores, mediante el término general:
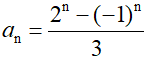
| a0=(1–1)/3=0 | a1=(2+1)/3=1 | a2=(4–1)/3=1 | a3=(8+1)/3=3 |
| a4=(16–1)/3=5 | a5=(32+1)/3=11 | a6=(64–1)/3=21 | a7=(128+1)/3=43 |
• Y otra forma de obtener los términos de esta sucesión, excepto el primero de ellos, es como sumas y diferencias alternas de potencias de 2:
| n=1 → a1 = 0 |
| n=2 → a2 = 20 = 1 |
| n=3 → a3 = 21 – 20 = 2 – 1 = 1 |
| n=4 → a4 = 22 – 21 + 20 = 4 – 2 + 1 = 3 |
| n=5 → a5 = 23 – 22 + 21 – 20 = 8 – 4 + 2 – 1 = 5 |
| n=6 → a6 = 24 – 23 + 22 – 21 + 20 = 16 – 8 + 4 – 2 + 1 = 11 |
| n=7 → a7 = 25 – 24 + 23 – 22 + 21 – 20 = 32 – 16 + 8 – 4 + 2 – 1 = 21 |
Esta relación se puede expresar de la forma:
Dos triángulos semejantes
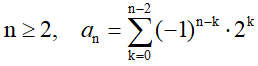
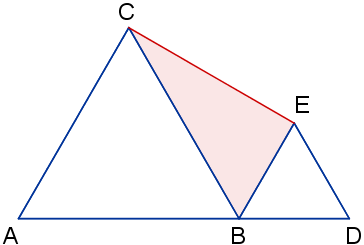
El triángulo ABC es un triángulo equilátero de 4 cm de lado. El triángulo BDE es un triángulo equilátero de 2 cm de lado Calcula la longitud del segmento CE y los ángulos del triángulo BCE.
Generaliza el resultado a todos los casos en los que el lado de uno de los triángulos es el doble del lado del otro.
Bifolium oblicuo
Curva de cuarto grado.
Haz «click» sobre la imagen para abrir la construcción de GeoGebra.
Más y más pequeño
M.C. Escher. Más y más pequeño. 1956.
Xilografía a contrafibra y fibra en negro y marrón. 20 × 30 cm.
Recubrimiento del plano con pentágonos
Utilizando pentágonos es imposible recubrir el plano. Según se observa en la figura, quedan huecos con forma de triángulo. Calcula la longitud del lado menor del triángulo sabiendo que el lado de cada uno de los pentágonos regulares es igual al número de oro.
Tipos de divisores
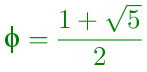
¿Qué números tienen todos sus divisores impares?
¿Qué números tienen todos sus divisores pares, sin contar el 1?
¿Qué números tienen la mitad de divisores pares y la mitad impares?
En el siguiente enlace puedes encontrar otra actividad sobre los divisores de un número: «Número de divisores«.
Infinito imposible
Otro infinito imposible de construir
