La distribución normal es la más importante de las distribuciones de probabilidad, dada la enorme frecuencia con que aparecen en las situaciones más variadas. Esta distribución evidencia cómo se comportan los valores de variables cuyos cambios obedecen a fenómenos aleatorios que podemos encontrar en materias como, biología y matemáticas, sobre todo, y donde las variables se comportan según una gráfica con forma de campana denominada campana de Gauss.
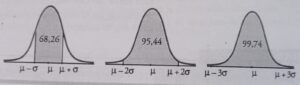
Así, variables como el peso o la talla de las personas, por ejemplo, se comportan atendiendo a esta distribución, donde los datos más bajos y los más altos, son más raros y se encuentran en ambos extremos. Mientras los datos intermedios, más frecuentes, se localizan en la zona central de la curva.
Para calcular la probabilidad de que ocurra un determinado evento, se de un determinado dato (peso, talla, etc…), calcularemos el área por debajo de la curva a partir de un determinado dato, lo que sería matemáticamente muy complejo. Para ayudarnos a conseguir este area, hacemos uso de la Tabla de la Normal.
En esta tabla se reflejan las probabilidades para distribuciones normales N (0, 1), o sea, distribuciones cuya media es 0 y su desviación típica es 1. Para distribuciones con otros datos de media y desviación típica, tendremos que convertirlas en distribuciones normales mediante una expresión matemática (enseñar como se hace esto, no es el cometido de este artículo). Una vez convertidos los datos de la distribución que buscamos, en una distribución normal, buscaremos los parámetros en nuestra tabla. Todos estos datos de conversión, el alumnado ciego lo hará con ayuda del editor científico “Edico”.
Para explicarles como se comportan las variables y el cálculo de probabilidades de una manera gráfica, usaremos el geoplano, con la ayuda de tornillos, gomillas de diferentes texturas y con goma-eva para delimitar las áreas a calcular. Con ello, podemos hacer que nuestro alumno invidente, tenga un claro concepto de la problemática a tratar.
Ahora bien, ¿cómo buscarán nuestro alumnado los parámetros de probabilidad?, ¿cómo usará la Tabla de la normal una persona ciega?.
Vamos primero a describir como usa un vidente la tabla de la Normal. Por ejemplo, para calcular la probabilidad de que se dé un suceso menor que este dato: 0,45. En la tabla tenemos dos entradas; vertical para unidades y décimas, y horizontal, para las centésimas. Para buscar la probabilidad de que se dé el suceso ≤ 0,45 (P[z ≤ 0,45]), buscamos en la entrada vertical el 0,4 y en la horizontal el 5 (ya que son 5 centésimas), el dato que está en la intersección de la fila y columna buscada, es 0,6736, o sea hay un 67,36% de que se dé el dato 0,45 o un dato por debajo de él.
Pues bien, para que el alumnado ciego pueda manejar la tabla de la Normal, podemos ofrecerle esta tabla creada en Excel.
Descárgate la tabla de Excel pinchando en este enlace
En un archivo Excel, nos encontraremos con dos entradas: la vertical descrita con números y la horizontal con letras. Al no tener, la hoja de cálculo, los valores 0, tanto en las verticales, como en las horizontales, e imprescindibles en esta tabla, procederemos de la siguiente forma:
Pongamos un ejemplo, vamos a buscar la probabilidad de que se dé el dato ≤ 0,48 (P[z ≤ 0,48]. Buscamos, en la entrada vertical, el índice que nos den (unidades y décimas), en nuestro caso 0,4. A este valor le quitamos la coma y le sumamos 1, para compensar la falta de la fila 0. Es decir, en lugar de buscar en la entrada vertical el 0,4 (correspondientes a las unidades y décimas, como hace el vidente), el alumno ciego buscará el 5, o sea 04+1.
Para buscar por la entrada horizontal, y aprovechando que el alumno ciego relaciona muy bien números con letras, debido a su sistema lectoescritor, en lugar de buscar 8 (centésimas), buscaremos la letra que corresponde a 8 más 1 (igualmente para compensar la falta de la columna 0), es decir H+1, por tanto, buscaremos en la entrada I (letra que corresponde al número 9). Y al buscar la celda I 5, obtendremos el parámetro buscado, que será 0,6844.
Si el problema que se le plantee a nuestro alumnado, es a la inversa, o sea dada una probabilidad concreta debe buscar el dato asociado a ella tendrá que restar 1 en ambas entradas. Así, por ejemplo si queremos calcular los datos cuyo parámetro en la tabla de la normal sea 0,9904, el alumno buscará en la tabla desplazándose bien vertical u horizontalmente, hasta llegar a este parámetro. Excel, con la ayuda del lector de pantalla Jaws, le dirá en que celda nos hemos encontrado este parámetro, en nuestro caso le dirá: E 24, o sea el parámetro 0,9904 está en la celda E 24, que corresponderá, en la unidades y décimas a 24-1, que al ponerle la coma será, 2,3, y para las centésimas: E, o sea 5-1, 4 (4 centésimas). Por tanto el dato que buscamos será 2,34.
De esta forma el alumnado ciego, mediante la tabla normal adaptada en Excel, podrá, al igual que sus compañeros, manejar estos parámetros para el cálculo de probabilidades de una distribución, y de una forma, relativamente sencilla.
Francisco Rodríguez Díaz.
Profesor Equipo Específico Atención al Alumnado con Discapacidad Visual Málaga.
